＜後編＞資産を最大限に増やすオプティマルｆの求め方とは？

＜後編＞

この本では、システムトレードに重要なマネジメントについて、
①システムの正しい選択
②適正なレバレッジの計算方法
③レバレッジとリターンの相関関係
を学ぶことができます。
そして、オプティマルｆに従った売買枚数は、資金が増えていく割合が最大　となるマネーマネジメントです。その実践方法が学べます。

また、本に基づきオプティマルｆの計算について、エクセルで計算シートで作成してみましたので、興味のある方はご活用下さい。

以下の記事は、この本を読んで重要だと思った個所を備忘録として、抜粋や自分の言葉でまとめたものです。そのため、理解が浅い部分や言葉足らずの記載もあると思いますので、鵜呑みにせず原本でご確認いただけると幸いです。

Table of Contents

第4章　最適固定比率トレーディング

最適固定比率

システムトレーディングをする場合、まず最初に考えなければならない事は、そのシステムに「正の期待値」が存在するかどうかである。次に考えることは、その正の期待値をどうすれば最大限に活用できるかである。

独立試行の場合で正の期待値のとき、最大損失の除数に用いられる0から1までの数値として表される最適固定比率（オプティマルｆ）が、各トレードにおける最適賭け率となる。

ｆ値は0～1で、上に凸のカーブとなる。

非対称レバレッジ

損失の穴埋めに必要な額は、損失の増加に伴い幾何的にぞうかする。

20％の損失：取り返すためには25％の上昇が必要
30％の損失：取り返すためには42％の上昇が必要
40％の損失：取り返すためには67％の上昇が必要

この関係を非対称レバレッジという。

オプティマルｆのピークは、損失を出したとしても、損失からうまく回復するために取るべき正しい枚数を指示する位置である。

●長年ギャンブル界では、オプティマルｆの求め方が研究されてきた。最も有名で正確なのがケリーの法則である。

ケリーの法則：最適賭け率が成長関数G（ｆ）を最大にする資産固定比率（ｆ）である。

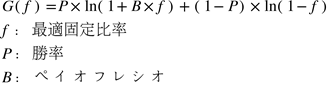
ケリーの公式

ベル研究所の技術者は、長距離データ通信のランダムなノイズとギャンブルのマネーマネージメントに関連する幾何的成長に多くの類似点を見つけた。ケリーの公式はこれらの研究から派生したものの一つである。

ケリーの第一公式

ｆ＝2ｘP-1
ｆ=最適固定比率
P=勝率

ただし、この公式は、「利益と損失が常に同額」の場合に使う。

ケリーの第二公式

ただし、この公式は、「利益が常に同額、損失も常に同額」の場合に使う。

＜幾何平均によるオプティマルｆの求め方＞

実際のトレーディングでは、トレードごとに利益も損失も異なるため、オプティマルｆの算出にケリーの公式は使えない。

HPRの公式をｆを含む式で表すと以下の様にになる。

これまでのまとめ

良いトレードシステムとは、幾何平均の高いシステムである。幾何平均を計算するためには、オプティマルｆの値を知らなければならない。

そのためのプロセスは、

システムのトレードリストを準備する。
TWRが最大になるオプティマルｆの値を求める。その方法は、試行錯誤法、反復収束法などで求める。
幾何平均は、求まったオプティマルｆ値でTWRのN乗根を算出する。（Nは総トレード数）幾何平均は他のマーケットシステムとの比較に用いることができる。ｆ値はそのシステムでトレードすべき枚数をきめるのに用いる。

TWRが最大になるf値が分かったら、それを金額に変換する。それは、最大損失を－ｆで割れば求まる。

（例）最大損失100＄で、オプティマルｆが0.25の場合、金額換算＝－100/－0.25＝400＄　となる。つまり、資金400＄につき1単位賭ければよいことを示している。

オプティマルｆは、常に1単位ずつ賭ける場合のシステムの収益性とリスクのバランスが最もよく取れた賭け率を表すものである。

＜スプレッドシートによる幾何平均の求め方＞

エクセルシートのダウンロード　

幾何平均トレード損益

幾何平均損益とは、毎回利益をを再投資し1トレードの1枚当たりの平均損益のことを言う。この値は、枚数が多い時の負けの影響、あるいは枚数が少ない時の勝ちの影響を示すものである。

幾何平均トレード損益は、1トレードの1枚当たりの期待値を金額換算したものである。

オプティマルｆのもっと簡単な求め方

エクセルシートのダウンロード

①トレード結果の挿入（最大損失は、自動算出）
②ｆのテスト値（仮のｆ値）を挿入
③f値の増分を変えてTWRの最大値を見つける
④TWRの最大となるｆ値がオプティマルｆである

オプティマルｆの利点

オプティマルｆは短期的にはさほど有効とは言えない。短期で奇跡的な成果を期待してはいけない。

トレード数が増えるほど、オプティマルｆを使ったトレードは、使わない場合との差は拡大するのである。

残された疑問点

正確なオプティマルｆを求めるためには、どの位のトレードサンプルが必要なのか？

任意の市場またはシステムのできるだけ長期にわたるトレーディングデータを用いるほど、そのデータから導き出されるオプティマルｆの値は将来のオプティマルｆの値に等しくなる。

オプティマルｆはどの位の頻度で計算しなおせばよいのか？

十分な長さのトレードデータ（30トレード以上）を使って計算したオプティマルｆは、著しく大きな利益または損失が生じない限り、トレードを行うたび毎に計算しなくても値が大きく変わることはほとんどない。

＜なぜオプティマルｆを知る必要があるのか？＞

ペイオフレシオが2：1の50/50のゲームでは、ｆ＝0.5でようやく収支が合う。ｆが0.5を上回った場合、破綻するのは時間の問題であることが分かる。

オプティマルｆから20％外れた場合、利益が1/10にも及ばないことがある。

オプティマルｆは正しい賭け金や正しいレバレッジを知ることができる。

ドローダウンは無意味、重要なのは最大損失

f=1.00を使ったとすると、最大損失が発生するとたちまち破産してしまう。
独立試行では、損益がどういった順序で発生した時にドローダウンが発生するかは一意てきに決まっていない。
固定比率トレーディングにおけるドローダウンは、一定枚数ベースによるトレーディングとは異なる。

ドローダウンとは極端なケースのことであり、それが何らかの意味のあるベンチマークとして使えるわけではない。なぜなら、独立試行では、ドローダウンが起きた後の確率は、それが起きる前と同じだからである。

ドローダウンのコントロールは不可能である。

一般に、優れたシステムほどｆの値は高い。ドローダウンはｆ値を下回ることは絶対ないので、f値が高いほどドローダウンは大きくなる。オプティマルｆは最大の幾何的成長を与えてくれると同時に大きなドローダウンを伴うものなのである。

オプティマルｆから外れすぎるとどうなるか？

オプティマルｆからの外れ度があまりにも大きければ、優位な状況にあっても必ず負ける。

f値が高すぎると、ドローダウンの損失も大きくなり、最適値に比べ、その回復に長い時間を要する。

ドローダウンは、どんな市場やシステムでも避けられない。しかし、オプティマルｆを使った資産カーブは、ドローダウンからの回復が早い。

最適固定比率から外れれば大きな代償を伴う。正しいf値を使うことは、システムの良し悪しよりも重要である。

成功率は、ポジションサイズをできるだけ頻繁に調整して、f値の指示するサイズにすれば高まる。

最適値より低いf値を使った場合、ドローダウンの大きさも小さくなりリスクは減るが、得られる利益も小さくなる。

つまり、f値が適正値から外れる場合は、小さい値の方が安全側になる。

放物線補間法によるオプティマルｆの求め方

探索領域に極値が一つだけ存在する場合は、放物線補間法が使える。

この方法は、X軸をｆ値、Y軸をTWR値で、横座標（頂点のf値）を3つの座標を次式に代入し求める。

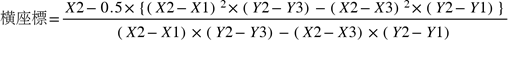
放物線補間法は、ｆカーブにひとつの放物線を重ね合わせ、入力座標を一つずつ変えながら放物線を描いていき、最新の放物線の横座標がその前の値に収束するまで続ける。

収束は、許容誤差（TOL)より小さいかどうかで判断する。通常、TOLは0.005を用いる。

プログラムは、付録Bに掲載。

オプティマルｆとオプション

オプティマルｆを統計的手法で求める。手計算では無理、コンピューターが必要。

算出方法は、本編Ｐ209～Ｐ217を参照。

驚くべき新事実。オプションを適当に購入したとしても、幾何平均が最も高い権利行使日までにオプティマルｆが示す枚数を購入すれば、期待値が正の状態を得ることができる。

期待値が正の状態は、「買いポジション」の場合であっても発生し得るのである。

第5章　破産確率

破産の定義：資金がゼロになりそれ以上トレーディングができない状態。

破産確率0：破産の可能性が無い

破産確率1：必ず破産する

公式

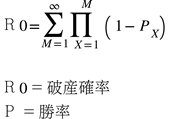
利益と損失が同額のときの破産確率（R1）

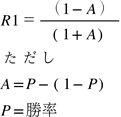
公平なマネーゲーム（勝ち1＄、負け-1＄、勝率50％）の場合

A=0.5-（1-0.5）＝0
R1=(1-0)/(1+0)=1

破算確率1で必ず破産する

投資資金の一部を投資する場合

これも公平なマネーゲームでは必ず破産する。

勝機を得るためには、期待値は必ず正でなければならない。

利益と損失が同額でない場合の破算確率の式（P・グリフィン　セオリー・オブ・ブラックジャックより）

エクセルシートのダウンロード

固定比率トレーディングにおける破算確率

固定比率トレーディングでは、理論上破産はありえない。現実のトレードでは取引の基本単位があるため、資金がそれ以下になったら破産となる。

破算確率の公式は、ギャンブル用に開発されたものであり、トレーディング用に開発されたものではない。ギャンブルは独立試行で定常分布に従うことを仮定しているが、トレーディングは非定常分布に従う。

破算確率とｆ

オプティマルｆを使っても破算確率を最小化することはできない。破算確率を最小にするベストな戦略は、トレードをしないことである。

破算確率の計算はトレーダーに安心感を与える程度のものでしかなく、それ以上の価値はほとんど無い。