<前編>
この本では、システムトレードに重要なマネジメントについて、
①システムの正しい選択
②適正なレバレッジの計算方法
③レバレッジとリターンの相関関係
を学ぶことができます。
そして、オプティマルfに従った売買枚数は、資金が増えていく割合が最大 となるマネーマネジメントです。その実践方法が学べます。
以下の記事は、この本を読んで重要だと思った個所を備忘録として、抜粋や自分の言葉でまとめたものです。そのため、理解が浅い部分や言葉足らずの記載もあると思いますので、鵜呑みにせず原本でご確認いただけると幸いです。
第1章 確率過程とギャンブル理論
確率過程においては、起こる事象を予測することはできないが、それぞれの事象が起こりえる確率は事前に知ることができる。
独立試行と従属試行
確率過程は2つのカテゴリーに分類できる。
①独立試行 : 事象の起こる確率が常に一定
②従属試行 : 前の事象が影響し事象ごとに確率が変わる
期待値

● 期待値が負の場合は、何度賭けても敗者にしかなれない。
起こり得る結果と標準偏差
標準空間:起こり得る事象列全体の集合
正規分布の標準偏差(SD)は次式で表される
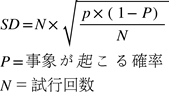
<正規分布>
全事象の68.26%が±1σの範囲に入る
全事象の95.45%が±2σの範囲に入る
全事象の99.73%が±3σの範囲に入る
● Nが増加すると標準偏差(SD)も増加する。これは、回数を増やすほど、全試行回数Nに対する比率で見た期待値に近づくことを意味する。=「平均の法則」
T:利益の総額
E:期待した利益
Nが増えれば増える程 T/N は E/N に近づく同時に EとNの差は拡大する。
ハウスアドバンテージ
● ハウスアドバンテージとは、カジノ側が常に有利になるようなルールのこと
● 5%のハウスアドバンテージがあるゲームでは、平均で5%の損失になる。つまり、独立試行を想定した場合の均等賭けでは、損失はハウスアドバンテージに等しいのである。
ゼロを下回る期待値は必ず破産を招く
● 期待値が負のゲームでは、どんなマネジメント理論を駆使しても、絶対に勝てない。賭けを続ければ必ず破産する。
決定指向と選択指向
● 最初にやるべきことは、正の期待値を見つけることである。これが数学的に正しいマネジメントの基本である。
選択指向:ファンダメンタルや直感に基づいて銘柄を選ぶような行為
決定指向:期待値が正の時にだけアクションを起こす。
確率過程における連勝と連敗
● 次に起こる事象が予測できないのと同じように、連勝や連敗も予測できない
従属性の有無
● 従属性がなければ、一連の勝ち負けの結果だけを基にパフォーマンスを改善しようとしても無意味であり、害はあっても利益は無い。
ランテスト、Zスコア、信頼度
● ランテストとは、システムトレードの連勝と連敗のZスコアを求めることである。
● Zスコアとは、データが正規分布の平均から何標準偏差の範囲内にあるかを示したもの。
● Zスコアが分かったら、次にそれを信頼度に換算する。
● ランテストにより任意のシステムから期待できる連勝(敗)数を求める。
● 連勝(敗)数が期待値と一致しない場合は、各トレード間に従属性がある。
<ランテストの方法とシステムのZスコアの求め方>
1.一連のトレードについてデータを集める
N=全トレード数
X=2x勝ちトレード数x負けトレード数
ラン数R=トレード開始から勝ち負けが交替する時点をカウントしたもの
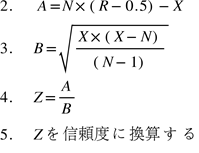
● Z<0 正の従属性がある。 連勝、連敗が起きる確率が高い。
● Z>0 負の従属性がある。 連勝、連敗が起きる確率が低い。
線形相関係数
● 従属関係、非従属関係を線形相関係数r(ピアソンのr)を使って数値化する。
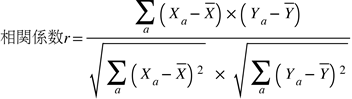
Yの値は、同じトレードを一つずつずらして2変数とする。
<先物トレードの場合>
● 強い正の相関がある時:r=0.25~0.30
大きな勝ち(負け)の後に大きな負け(勝ち)が続くことはほとんど無い
● 強い負の相関がある時:r=-0.25~-0.30
大きな勝ち(負け)の後に大きな負け(勝ち)が続く傾向が強い
第2章 システムと最適化
システムと最適化
● トレーディングでは、テスト済みの完全にメカニカルなシステムが不可欠である。
● メカニカルなルールを使わずに長期にわたって勝ち続けることは、何人といえど不可能である。
● 良いシステムがあっても、きちんとしたマネーマネージメントの考え方が無ければうまきいかない。
● パフォーマンス向上ためには、システムそのものよりマネーマネージメントのほうがはるかに重要である。
● マネーマネージメントを生かすためには、勝てるシステム(期待値が正)が必要である。
● システムの検証は、・最低5年 で ・手数料と・スリッページ を引いてもパフォーマンスが許容できること。
● 過去のデータを基に作成されたシステムは、最適化され過ぎている。
● 最適化は誤用が危険。非最適化を賢く利用する。
システムのパフォーマンスの測定
①プロフィットファクタ(PF)
PF=利益合計/損失合計
または、
![]()
W%:勝ちトレード比率
L%:負けトレード比率
AW:平均勝ちトレード額
AL:平均負けトレード額
②悲観的リターンレシオ(PRR)
PRRは信頼性に高いデータほど良い値になる。
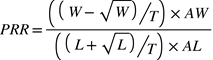
W:勝ちトレード数
L:負けトレード数
T:全トレード数
AW:平均勝ちトレード額
AL:平均負けトレード額
N無限大の時、PRR=PF
PRR>2.0 とても良いシステム
PRR>2.5 非常に優れたシステム
非最適化
<非最適化のルール>
①できるだけ長期にわたるデータセットを使って最適化する。
②用いるパラメータの数はできるだけ少なくする。
③パラメータに左右されない堅牢なシステムを選ぶ。
パラメータパラメータ値の変動に鈍感なシステムの方が好ましい
堅牢性の確認:PRRとパラメータのグラフを用いるのが一般的
パラメータ値、期間、市場に左右されないかどうか
④フォワードテストを行う
⑤パフォーマンスが最大となる領域を見つけ、その中では、最低となるパラメータ値を選ぶ
● 非最適化したあとでも良いシステムは、手を加えてはいけない。
第3章 利益の再投資と幾何的成長
利益の再投資と幾何的成長
トレーディングで得た利益を再投資すべきか否か
● トレーディングで得た利益を再投資した場合、勝てるシステムが負けるシステムに転じることはあっても、その逆は無い。
● 最終的な結果は、トレードの順番に影響されない。
● しかし、システムが十分に優れていれば、再投資の方が、得られる利益ははるかに大きく、利益の差は時間と共に拡大する(複利効果)。
『幾何平均』 再投資で利益のでるシステムかどうか判定する
TWR:最終資産比率
● TWRの幾何平均が再投資のパフォーマンス測定に適している
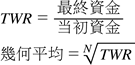
N=総トレード数
● 幾何平均は、1取引当たりの資金の成長率を示す。
● 幾何平均が最大となるシステムや市場ならば、利益再投資で利益を得る事ができる。
● 幾何平均<1 ならば、再投資で損失することを意味する。
<幾何平均の概算方法>

ベストな再投資方法
<マネーマネージメントの基本>
● 独立試行では、期待値が0以下の場合、どんなマネーマネージメント、どんな掛け方、掛ける順序を変えても、その期待値を0以上にすることはできない。
<マネーマネージメント戦略を考える上での重要な4つのポイント>
① 有利なトレードでは、数学的に可能な最高額を稼がなければならない。
② 資金の成長率と安全性とのトレードオフも考慮しなければならない。
③ 勝つ見込みがあるかどうかを考慮しなければならない。
④ トレードサイズは勝った時に得られる額と負けた時に失う額とに照らして決めなければならない。
● 昔からギャンブラー達は様々な「賭け方(戦略)」を試してきた。
・マーチンゲール戦略
・スモールマーチンゲール戦略
・逆マーチンゲール戦略
・ベース+利益の一部を賭ける戦略(リザーブ戦略)
・ベース+利益の平方根を賭ける戦略
● 多くの人に、負けや連敗、ドローダウンの後に枚数を増やす傾向が見られるが、マネーマネージメントの方法としては、非常にお粗末である。
● コンピューターシミュレーションでは、プレーヤーに有利な独立試行では、資金の増加に応じて賭け金を増やすのがよく、ベットサイズは総資金の一定比率するのが最適と導き出した。
●「ギャンブリング・タイムズ」誌1987.6号で、ウィリアム・T・ジェンバは一定比率賭けが他のどの賭け方戦略よりも優れていると発表した。